2018-05-29

文案 | 转录调控事业部
小伙伴儿们在拿到转录组结题报告后,会发现一张名为PCA的主成分分析图,如下所示:
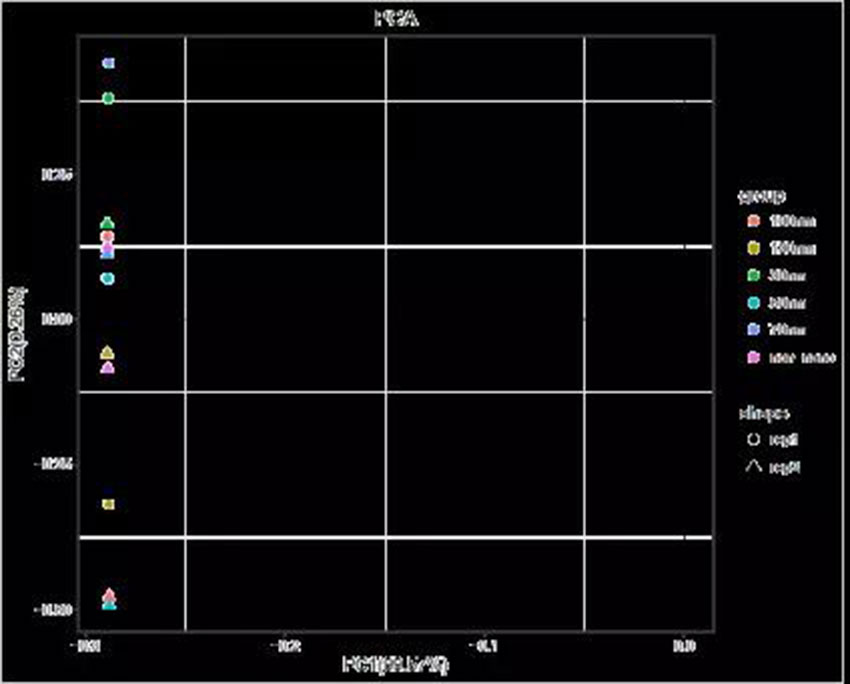
PCA图到底代表什么意义?是怎么得到的?
今天我们一一阐明。
PCA(Principal Component Analysis)官方定义如下:
是一种通过线性变换将原始数据变换为一组各维度线性无关表示的数据分析方法。
对于没有相关背景的童鞋们来说,看完定义好像更加摸不着头脑了。让我们先用社会通用语翻译一下这个定义:PCA算法主要是用于提取大数据的主要特征分量,又称为主成分分析。

那主成分又是什么概念呢?
要搞明白数据的主成分,就不得不从数据降维说起。数据降维也是PCA分析的思想。
举个简单直观的例子:假设三维空间中有一系列点,这些点分布在一个过原点的斜面上,如果用自然坐标系x,y,z这三个轴来表示这组数据的话,需要使用三个维度。这时我们把x,y,z坐标系旋转一下,使数据所在平面与x,y平面重合,把旋转后的坐标系记为x',y',z',那么这组数据的表示只用x'和y'两个维度表示即可。即从三维降到了二维。
我们都知道,三点一定共面,也就是说三维空间中任意三点中心化后都是线性相关的,按照这个思路而言,n维空间中的n个点一定能在一个k(k<n)维空间中分析。
降维意味着信息的丢失,为了尽力将信息的损失尽量降低,我们鉴于实际数据本身常常存在的相关性,可以选择k维空间中累计贡献度最大的前两个向量作为数据源进行降维分析,最终得到主成分Y1、Y2,主成分定义如下:
设X =( x1, x2,…… xp)’是p维随机向量,二阶矩存在。若向量t1’=(*11,*12……t*1P) 在|t1|= 1的条件下使得Varp(t'1X) 最大, 则称Y1 =t'1X 是X的第一主成分或第一主分量; 若向量t2’=(*21,*22……t*2P)在|t2|=1; Cov(t'2X, Y1)=0的条件下使得Varp(t'2X) 最大,则称Y2 =t'2X 是X的第二主成分或第二主分量。
好了,理论知识准备好了,回到我们最初的目的上来,我们拿到了一组转录组数据,每一个检测到的基因都有一个表达量数值(FPKM/RPKM/TPM),所有基因的表达量都在二维空间中转化为一组向量,假设我们此次检测到一万个基因,那理论上全部数据的空间分布可能涉及到一万个维度,根据我们的降维思路,n维空间中的n个点一定能在一个k(k<n)维空间中分析,我们就可以通过线性变换将高维数据最终压缩到第一、第二特征分量所在的二维平面上,最终得到我们看到的以PC1、PC2展示的图片效果。
关于PCA的降维思想,你get到了吗?


